SOL: HOWEVER WHEN POLITIONS ARE ASKED A QUESTION THEIR "STALL SPEED" IS MATHEMATICALLY IMPOSSIBLE TO CALCULATE!

http://www.paulcraigroberts.org/2015/12/01/an-experienced-pilot-explains-stall-speed/

An Experienced Pilot Explains “Stall Speed”

December 1, 2015 | Categories: Articles & Columns | Tags: |  Print This Article

The Airplane Aerodynamic Stall Explained

In the aftermath of the downing by Turkish F-16 fighter jets of the Russian Sukhoi tactical bomber Su-24 over Syria, some have pointed out that Turkish claims the Russian jet was in Turkish airspace for 17 seconds, but covered a distance of only 1.15 miles, would imply the Russian jet would have had to be flying at only 243 mph, which some say would be slower than the airplane’s stall speed and therefore impossible.

Others dispute this stall speed figure and say an airplane of this type would have a stall speed closer to 150 mph. Who is right, and how can we find some objective answers? We can and we will.

The most important point is that there is no such thing as a single stall speed for any airplane, as Dr. Roberts pointed out. In fact wing stall is not a function of airspeed, but of the wing’s angle of incidence to the oncoming airflow, which is called the angle of attack (AoA) or simply alpha (this angle is obviously a function of the airplane’s “attitude” or pitch-up angle).

If wing angle of attack exceeds the critical point, the airflow starts to separate from the top surface of the wing (the suction side), and the wing will begin to lose lift and a stall recovery maneuver is required.

The stalling angle of most airplanes is on the order of 15 to 18 degrees of angle of attack, although some combat aircraft have special design features, such as leading edge root extensions (or LERX) that may increase critical AoA to about 30 degrees. Engine power plays a big role too—a fighter aircraft with very powerful engines and low airplane weight can sustain high angles of attack by using its engine power to overcome the loss of lift due to wing stall.

It is also useful to know that wing lift increases nearly linearly with an increase in the angle of attack. So if we want to double lift, we must double the angle of attack.

For example when taking off, the pilot will pull back on the control yoke and increase the pitch-up angle of the airplane, thus increasing angle of attack and thereby total wing lift. The extra lift launches the airplane into the air!

This maneuver is called takeoff “rotation” which refers to the pilot in effect rotating the aircraft about its pitch axis (which can be thought to run horizontally from wingtip to wingtip).

It is an old truism that every student pilot is taught early on, that any airplane will stall at any speed, at any attitude, and any bank angle. So when we say that an airplane has a certain stall speed, it is simplifying things to the point of uselessness.

As Dr. Roberts pointed out, an airplane that is maneuvering can have a higher stall speed than if it is simply flying straight and level. When an airplane is in a banked turn the lift created by the wing is also tilted, since lift is always perpendicular to the wing. If the airplane is banked at 45 degrees, it means its lift vector will be pointing 45 degrees from the vertical (or horizontal if you prefer), as seen in the figure below.

The wing’s lift in a bank decreases by the cosine of the bank angle. If the airplane is banked 45 degrees, the cosine is 0.707 and the amount of vertical lift is only about 70 percent of the total lift that is now pointing at 45 degrees.

In order to maintain the airplane’s altitude in a turn, the pilot must then pull back on the yoke and increase the angle of attack, so as to increase diagonal lift and thereby provide enough vertical lift component to maintain the aircraft at the same altitude. That vertical lift component is shown in the diagram.

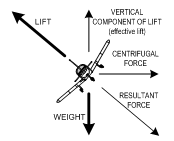
It should be noted that the airplane loses lift exponentially with increasing bank angle. In a 60 degree bank the cosine is 0.5, (which is 0.707squared). At this bank angle the vertical lift component is now only half of the total diagonal lift, and the airplane now needs double the lift it would normally need at straight and level flight. Again the pilot has to pull back the yoke and increase airplane pitch attitude to an angle of attack about double what it would be in straight and level flight.

In a 75 degree bank the cosine is 0.26 which means the airplane now needs almost four times as much lift. Pitching the airplane into such an attitude could well exceed the critical angle of attack and bring about wing stall—which could be dangerous at such a steep bank angle.

Now it should be noted that all the above examples of airplane bank are assumed for a level turn, where the aircraft stays at the same altitude. This is the “standard” turn maneuver. If the airplane were to simultaneously bank and descend, there need not be any loss of lift (depending on bank angle and rate of descent), although the pilot must now be careful that the descending airplane does not overspeed, or enter a dangerous spiral dive.

Another technical point worth noting in turning maneuvers is that (in a level turn), the airplane (and pilot) weight increases due to centrifugal force, just as you may remember as a child on those spin rides, where you felt heavy and unable to move your arms or legs.

In a level turn the g loading is simply the inverse of our above bank-to-lift relation—ie. g = 1 / cosine bank angle.

If the bank angle is 45 degrees the cosine is 0.7 and the g-loading is therefore 1 / 0.7 = 1.41. In other words, if the pilot weighs 100 pounds, she would now feel as if she weighed 141 lb. The aircraft’s effective weight would be 1.41 times greater.

In a 60 degree turn g-loading is 2, so the plane and pilot’s weight is effectively doubled. In a 75 degree turn the g-loading is 3.9, which means that 100 lb pilot would feel like she weighs 390 lb, and the airplane is nearly four times as heavy (at least as far as the unforgiving force of gravity is concerned). Again, this kind of steep bank angle would likely result in a wing stall.

Another important point to consider is altitude, which determines the air density. The higher the altitude, the lower the density (due to less air pushing down from above) and the higher the stall speed.

Let’s first consider the “standard” published stall speed, Vs, which is typically given for landing and takeoff conditions at sea level standard day conditions, which means 15 C (59 F) and atmospheric pressure of 101.3 kilopascals or 29.92 inches of mercury.

At high altitude and thinner air, the stall speed can approach or even surpass the airplane cruise speed! A friend has flown hundreds of USAF missions in the Lockheed U2 reconnaissance airplane, considered the highest-flying jet in the world. The aircraft’s cruise speed in that thin air at over 65,000 feet altitude is only several mph above its stall speed, requiring constant pilot attention to keep the aircraft in its very narrow safe operating speed range.

That is because the air molecules are so few and far between that the pilot must fly at a high angle of attack just to keep aloft. If he loses his concentration and the speed drops only slightly, the airplane wing will stall, and a recovery under those conditions might be very difficult.

In pilot circles this flight regime is known as the coffin corner. There have been a number of deadly crashes of high performance aircraft at high altitudes, prompting the FAA to issue an advisory on high altitude flight.

Now there is a mathematical formula that relates stall speed and air density:

Stall Speed = the square root of wing loading (which is the aircraft’s weight divided by its wing surface area), times 2, divided by air density, and divided again by the wing’s maximum lift coefficient. In mathematical terms the formula looks like this:

Vstall = sqrt( (W/S) * 2 / rho / CLmax)

Where W/S is the wing loading (or airplane Weight divided by wing Surface), rho is the air density and CLmax is the maximum lift coefficient.

So we can see just by looking at that relation that the lower the air density, the higher the stall speed will be.

Published data on the Su-24 stall speed is difficult to find, but we can make an educated guess using a typical estimate of maximum lift coefficient for combat aircraft that ranges between 1.2 and 1.8—in the so-called clean configuration, ie. no high lift devices like landing flaps extended. In normal flight the aircraft would be flying clean to reduce drag, but might deploy flaps in a tight turn to increase its lift and help prevent stall.

If we assume the CLmax is between those given values, say 1.5, then we can work out the rest since we know the airplane’s wing loading is 133 lb / ft ^2 (wikipedia) and we know the airplane was flying at about 6,000 meters altitude, about 19,700 ft. At this altitude air density is only about half of what it is at sea level: in metric the air density on a “standard” day at that altitude would be about 0.66 kg per cubic meter, or in English units, 0.00128 slugs per cubic foot, where 1 slug equals 32.2 lb; (32.2 feet per second being the acceleration of gravity on earth).

So if we plug in the numbers we get:

sqrt(133 * 2 / 0.00128 / 1.5) = 372 feet per second.

To convert to mph we multiply by 15 and divide by 22 and get 253 mph as our stall speed at straight and level flight at 6000 meters altitude, about 19,700 ft. Now any turning or banking maneuver would obviously increase stall speed further, so we can think of 253 mph as a minimum flying speed at that altitude for the Su-24 (again assuming standard day conditions).

Now that wing loading assumes a fully loaded aircraft, which probably was not the case. The Sukhoi would likely not have been carrying full fuel of about 11 tons (22,000 lb), although it might have been carrying its complete payload of over 3 tons of ordnance (6,000 lb). However reports of the sortie described the pair of bombers had already made one bombing run, so full ordnance was probably not on board either.

We can take a stab at estimating the operating weight of the aircraft at that time. The Su-24’s empty weight is published as just under 50,000 lb (wikipedia). If we assume half fuel, that would be about 11,000 lb, and if we assume half ordnance load, that would be about 3,000 lb, giving a total aircraft weight of 64.000 lb.

The published wing area is 594 square feet, so the wing loading under this flying condition would be 64,000 / 594 = ~108 lb/ft^2.

If we now plug that into our stalling equation that takes into account the air density, we get:

Vstall = sqrt(108 * 2 / 0.00128 / 1.5) = ~335 fps, which equals ~227 mph.

Again, this is an approximation of the Su-24 stalling speed at part-weight and straight and level flight at 19,700 ft altitude. Any turning maneuver would increase stall speed as described above. Also a warmer than standard temperature at that altitude would lower air density (and increase the effective altitude). This is known as density altitude and all pilots are trained to work only with density altitude, since non-standard meteorological conditions are not uncommon.

Note also that the actual CLmax value of the Su-24 may be something different than our guesstimate; a higher value would decrease the stall speed, but a lower value would increase it. We are making an educated guess. However, this puts us in the ballpark and hopefully sheds some light on the technical issue under dispute.

On a practical level, it is outside the realm of possibility that a bomber aircraft would be flying at the edge of its stall at any time during a sortie, other than hard evasive maneuvers to avoid enemy action. Since the rescued co-pilot reports that they did not even see the missile coming, nor had time to take evasive maneuvers, it can be assumed with strong certainty that the airplane would not have been flying near the stall at any time.

More than likely the aircraft would have been flying in the so-called “transonic” regime where airliners usually operate, which is about 550 to 650 mph.

In light of this brief and inexact analysis, there appears to be reasonable doubt as to the Turkish version of the Sukhoi’s incursion into sovereign airspace under the conditions described.

Dr. Paul Craig Roberts was Assistant Secretary of the Treasury for Economic Policy and associate editor of the Wall Street Journal. He was columnist for Business Week, Scripps Howard News Service, and Creators Syndicate. He has had many university appointments. His internet columns have attracted a worldwide following. Roberts' latest books are The Failure of Laissez Faire Capitalism and Economic Dissolution of the West and How America Was Lost.